Steeds vaker hoort men in het nieuws dat wetenschappers of statistici bepaalde voorspellingen doen. Een van de bekendste is de uitermate goede voorspelling van Nate Silver over de verkiezingsuitslag per staat in de Verenigde Staten in 2012. Ook nu is Nate Silver hard bezig met zijn voorspelling voor de huidige wedloop tussen Trump en Clinton.
Buiten beschouwing gelaten of ze het wel altijd bij het rechte eind hebben, is het toch interessant deze voorspellingen eens nader te bekijken. Want hoe gaat dat nou in zijn werk? In dit blog gaan we een van de intuïtief meest logische, en ook vaakst gebruikte, predictie methoden bekijken op inmiddels bekend terrein: De Olympische Spelen.
Wij hebben een voorbeeld dataset gemaakt, dat het aantal medailles voor de zomerspelen per land bevat. We beperken ons tot de spelen vanaf 1996, en per zomerspelen alleen de top 20 landen met de meeste medailles. Deze dataset hebben wij vervolgens verrijkt met het bruto binnenlands product per hoofd van de bevolking (BBP) en het verloop van de bevolkingsaantallen van de desbetreffende landen.
De populatie data hebben wij van United Nations World Population Prospects 2015. Het aantal medailles en het BBP is van Wikipedia gehaald.
Aan de slag
Hoe zou jij zelf het aantal medailles voorspellen voor een land? Het eerste waar je misschien aan denkt is waarschijnlijk te kijken naar resultaten behaald in het verleden: de vijf zomerspelen van 1996 t/m 2012 vertellen ons al hoeveel medailles wij als land hebben gehaald, namelijk 19 in 1996, 25 in 2000, 22 in 2004, 16 in 2008 en 20 medailles in 2012 (figuur 1). Het meest eenvoudige predictiemodel is dan ook om het gemiddelde te nemen van deze reeks: dat is dan 20 medailles.
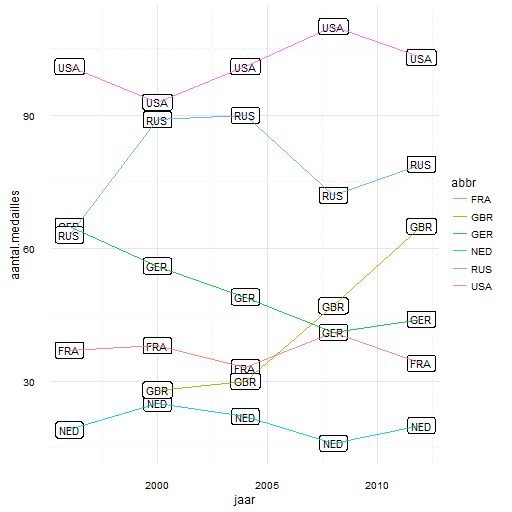
Figuur 1: het verloop van het aantal medailles over de afgelopen 5 zomerspelen voor een selectie van landen.
Een volgende stap zou zijn om ook de trend (toename of afname van aantal medailles) mee te nemen in ons model. Deze trend kunnen we doortrekken tot 2016 om een predictie te doen (figuur 2 – gekleurde ovaaltjes zijn de predicties).

Figuur 2: Een lineaire trend-lijn dat het aantal medailles zo goed mogelijk benaderd. Deze lineaire trend-lijn is doorgetrokken om een voorspelling te doen over 2016.
Data voor predictie
We hebben nu al twee factoren meegenomen: het aantal medailles behaald in het verleden en de verandering van dit aantal in de tijd. In essentie is dat waar statistische predictie op gebaseerd is: gebruik van beschikbare data om iets over de toekomst te kunnen zeggen. Kunnen we een betere predictie doen met meer data?
Zoals aan figuur 2 te zien is, is ons model niet perfect; de lineaire benadering van het aantal medailles behaald per land over de afgelopen 5 zomerspelen zit er ruim tientallen medailles naast. Alhoewel Nederland zo stabiel is qua medailles dat dit voor ons land wel meevalt! Ons eerste model is dus waarschijnlijk al aardig!
Maar laten we proberen het beter te doen. Als eerste gebruiken we een niet-lineair model (figuur 3). Dit leidt tot een betere benadering van ons model tot het werkelijk aantal behaalde medailles (dit hoeft niet per sé tot een betere predictie te leiden overigens!).

Figuur 3: Gebruikmakend van een niet-linear model kunnen we het aantal werkelijk behaalde medailles beter met een model benaderen. En wellicht ook beter iets over de toekomst zeggen.
Gebruik makend van ons gezond verstand, gaan we op zoek naar meer data die invloed zou kunnen hebben op het presteren van een land op de Olympische spelen.
- Een rijk land zal meer inwoners hebben die de mogelijkheid hebben een sport te beoefenen.
- Een land met veel inwoners zal waarschijnlijk meer mensen met topsport talent bezitten.
Laten we eens naar deze twee datasets kijken in figuur 4 en 5. Inderdaad, er is een positieve trend voor populatie en voor het BNP, wellicht helpen deze in onze predictie! Het visualiseren van meer dan 2 factoren die meedoen in onze voorspelling is niet echt praktisch. Het uiteindelijk voorspelde aantal medailles en de benadering van het model over het historisch aantal medailles echter wel (figuur 6).
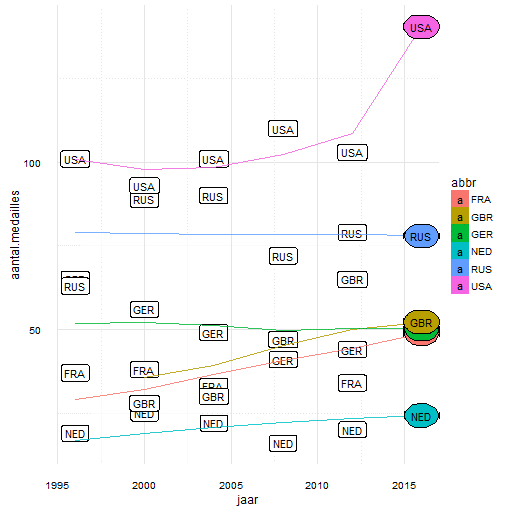
Figuur 6: Onze voorspelling voor het aantal medailles in 2016: Vooral de V.S. gaat het erg goed doen!
Onze ‘voorspelling’
Ons predictiemodel voorspelt, gebruikmakend van historische behaalde medailles, populatie, en BNP per hoofd dat Nederland 24 medailles behaald. Ook opmerkelijk is het enorme aantal van de VS: 141 medailles!
Het resultaat.
Blijkbaar zijn we vooral voor Rusland iets in ons model vergeten mee te nemen! Met slechts 56 medailles is het flink gezakt! Natuurlijk zijn dit juist situaties waar statistische modellen vaak slecht in zijn: uitzonderingen! Er is namelijk helemaal niets over doping risico’s in ons model opgenomen.
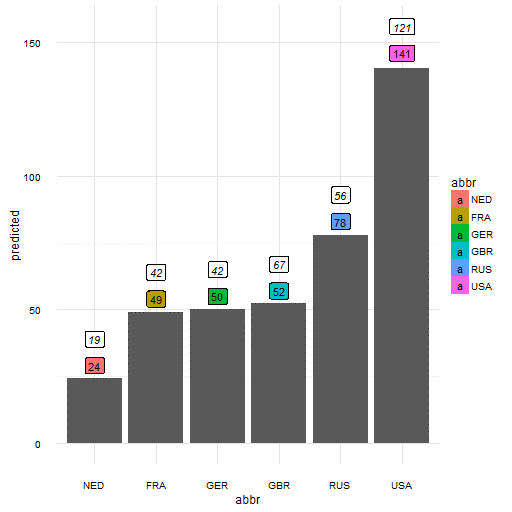
Figuur 7a: Het volledig predictiemodel (met de voorspelling in gekleurde vakjes en de werkelijke getallen erboven).
Bovendien kan men een dergelijk vereenvoudigd model niet al te serieus nemen; het verschil in BBP en populatie van een land in 4 jaar zal nooit genoeg extra informatie leveren om de predictie enorm te verbeteren dan een model alleen gebaseerd op medaille-aantal trend of medaille gemiddelden.
Dit is goed te zien in de predictieresultaten van figuur 7b; onze predictie zonder BBP en populatie van figuur 3 – heeft het aanzienlijk beter gedaan dan de meer gecompliceerde versie van figuur 6, waarvan het resultaat in getallen wordt getoond in figuur 7a. Dit verschijnsel heet ‘overfitting’ en is een bekend probleem bij predictiemodellen: er zijn zoveel variabelen die mee doen in de voorspelling dat de werkelijke waarden zeer goed benaderd worden, maar ten koste van de predictie! Meestal wordt dit voorkomen met een methodologie genaamd ‘cross validate’, maar daarover kunnen we met gemak een nieuw blog vullen.
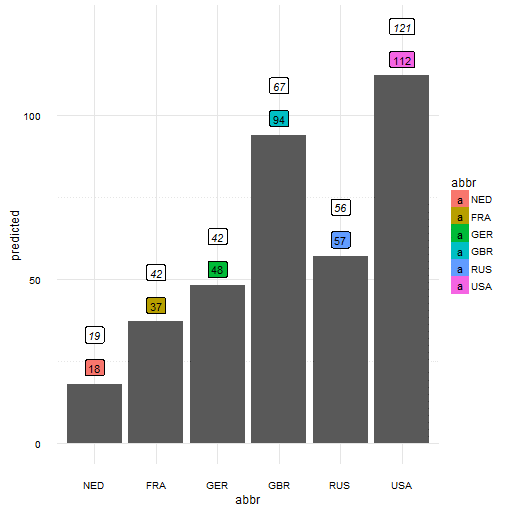
Figuur 7b: Het predictiemodel zonder BBP en de populatie (met de voorspelling in gekleurde vakjes en de werkelijke getallen erboven).
Wellicht zouden variabelen zoals het 4 jaren budget dat een land aan topsport investeert en het land dat de spelen organiseert (thuisvoordeel) meer informatie kunnen leveren voor predictie.
Verdere mogelijkheden
Voor betere, of meer geavanceerde analyses kunnen andere statistische methoden gebruikt worden. Denk daarbij bijvoorbeeld aan deep-learning, zoals Google onlangs heeft toegepast met AlphaGo, het programma dat onlangs de wereldkampioen GO met 4-1 versloeg.
Maar ook data van een andere granulariteit kan gebruikt worden. Denk bijvoorbeeld aan een dataset waarbij per sporter geanalyseerd wordt, op basis van eigenschappen als behaalde resultaten, consistentie, prestatie onder druk en looptijden. Elke sporter krijgt zo een berekende statistische kans om een bepaalde medaille te behalen. Een dergelijk model zou wellicht veel beter presteren, maar zou tegelijkertijd ook veel meer tijd kosten: Die afweging tussen de kosten en baten is een onderdeel van elk project waarin statistiek een rol speelt.
Er zijn praktijkvoorbeelden waarin dit soort gedetailleerde modellen gebruikt worden. Een bekend voorbeeld daarvan is bijvoorbeeld bij het in kaart brengen van de eigenschappen of het koopgedrag van consumenten voor meer specifieke marketing.
