 In Part I of my Practical Analysis series on analysis and statistics, I talked about statistical concepts. Understanding the concepts is essential, but we also need to know the tools to put them to work. Here we discuss tools for applying statistical concepts and the importance of using the right tool at the right time.
In Part I of my Practical Analysis series on analysis and statistics, I talked about statistical concepts. Understanding the concepts is essential, but we also need to know the tools to put them to work. Here we discuss tools for applying statistical concepts and the importance of using the right tool at the right time.
There are two sides to what we do with these tools. As analysts, we can think of ourselves as members of a team competing to prove the truth. We’ll call this “the game.” The defensive side is working to defend our claims, using our tools and data. On offense, we work to refute the opposing team’s claims – at least when they differ from ours. The theories of Statistics provide the rules and boundaries of the game.
Using Deborah Rumsey’s books “Statistics for Dummies I & II” for background, let’s look at a few particularly useful tools in an analyst’s toolbox.
Standard Deviation
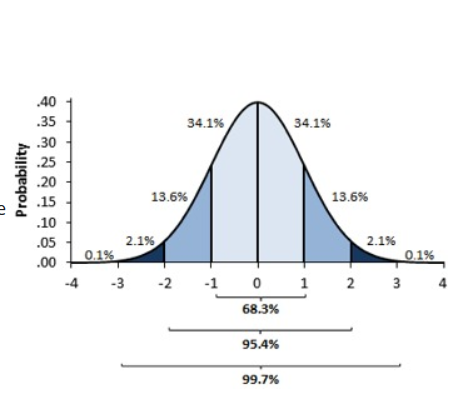
Standard deviation provides a truly useful perspective on a population with a normal distribution. Picture the bell shape of the normal distribution: most of the population lies close to the center – or mean. The “empirical rule” of 68-95-99.7 states that 68% of the observations in the population fall within one standard deviation (plus or minus) of the mean; 95% lie within two standard deviations; and 99.7 within three. That allows you to easily spot outliers. Any observation beyond — or even close to — two standard deviations is likely to be an outlier and not typical of the population.
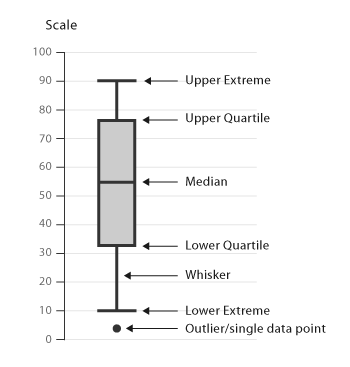
Quartile Box Plots
To help visualize rank and relative standing, we can plot a population on a chart that shows how quartiles are distributed. Quartiles are the values that divide a list of numbers into quarters. Imagine putting a list of numbers in order, then cutting the list into four equal parts. The quartiles are at the “cuts” and the second quartile is the median.
In a quartile box plot, a vertical box is divided into two segments with lines extending above and below to represent the minimum and maximum values (excluding true outliers). The length of the segments tells you how much variation there is in the population as well as whether it is skewed to one side or another – in other words, not normal. The mean and the median tell us about the central tendency and help determine the symmetry of the distribution. If the mean and median are close, the distribution likely is normal, or at least not skewed. There’s even a tabular version of this called the “five-number summary” for those who prefer numbers to pictures! This can yield useful insights with minimal math.
There is a more advanced set of tools covered in “Statistics for Dummies II” that helps us take our analysis to the next level. But once again it is important to know when to use which tools. To start, consider whether we are dealing with categorical or quantitative data. We can use statistical techniques to estimate, make comparisons, explore relationships, and predict values with either type of data, but the techniques are subtly different.
Categorical variables
Categorical variables are qualitative in that they can be classified into groups with a single observation only belonging to one group, such as blue, green, or brown eyes. They have no inherent numerical value. For categorical data, we use margin of error to estimate proportions of a population, such as the percentage of women voting for a particular political candidate. Our estimate is described as falling within a likely range, such as plus or minus three percentage points of the estimate. If we’re analyzing potential relationships between multiple categorical variables, such as the how men and women vote by political party, we use a two-way table and the Chi Square test. And if we’re trying to predict a categorical outcome which only has two possible values, we create predictive models using logistic regression.
Quantitative variables
Quantitative variables are represented by numbers, such as cost or number of trips. When estimating quantitative data, we use numerical units instead of percentages. For example, the mean value of a single-family home in a certain community might be $250,000 with a margin of error of $15,000. With quantitative data, we use t-tests to compare two populations, such as the average income of men versus women, and we apply analysis of variance when more than two populations are in play.
Linear regression allows us to assess the degree of correlation between quantitative variables and predict values based on correlation where it exists. There are several variations of regression analysis available for when the basic form doesn’t do the trick. Multiple regression allows us to use more than one variable to predict an outcome. Non-linear regression works when the correlation relationship is something other than a straight line. And there are combinations of the two — lots of possibilities, to say the least.
Finally, some populations don’t have a normal distribution. For these, we can employ non-parametric techniques that use the median, instead of mean, and the rank order of observations, rather than standard deviation. This is important if you deal with data that tends to be skewed. You don’t want the other team to catch you relying on techniques that assume a normal distribution when it doesn’t exist. Flag on the field!
This summary doesn’t do justice to the nearly 700 pages in Deborah Rumsey’s two books, but I do hope it will give you an idea of what is in an analyst’s statistical toolbox and inspire you to explore further.
Read other articles in the Practical Analysis blog series
- Numeracy: Analytical Skills for the 21st Century
- Practical Analysis: Learning from the Experts
- Practical Analysis: How Statistics Help Us See the “Gray”
- Practical Analysis: The Next Chapter - May 21, 2020
- Exploratory Data Analysis Part 2: Helping You Make Better Decisions - October 11, 2019
- Practical Analysis: Understanding Visualization Concepts - September 19, 2019

